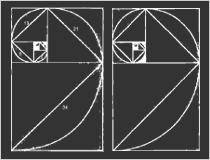
Spirale d’Or

"Quiconque cultive la règle d’or du juste milieu se préserve du misérable toit délabré et du palais trop envié."
(Poète de la Rome antique)

Spirale d’Or or	Spirale d’Or argent

la forme de la Spirale d’Or

La structure de la Spirale d’Or représente deux formes très connues de la géométrie sacrée : la spirale du nombre d’or (phi) et la spirale de Fibonacci. Elle est la base de la forme d’un crop circle connu sous le nom de "Formation ou Cercle de Hackpen Hill" qui est apparu dans un champ de blé anglais en 1999.  

Phi (nombre d’or) - "La clé de la physique du cosmos" (Platon)

Phi est une valeur constante qui est encore plus mystérieuse et profonde que pi dans ce qu’elle implique. Comme pi, phi est un nombre irrationnel qui n’a pas de solution arithmétique. les décimales se poursuivent à l’infini sans se répéter. Ce qui rend ce nombre unique est le fait qu’il soit incorporé dans toutes les structures organiques connues. De la structure osseuse de l’être humain, en passant par la disposition des graines d’un tournesol jusqu’à la spirale d’un coquillage, la proportion phi est présente, sous-jacente à toute structure biologique, semblant être un modèle géométrique de la vie elle-même.


Platon est allé jusqu’à appeler la proportion phi la "clé de la physique du cosmos". Phi est calculé au 1.6180339+…, et alors qu’il ne peut être résolu arithmétiquement, on l’obtient facilement à l’aide d’un compas et d’une règle.

Le nombre d’or en architecture

La proportion phi se retrouve dans l’architecture de la Grande Pyramide, dans le triangle formé par la hauteur, le demi-côté de la base et l’apothème, ou diagonale. En d’autres termes, la coupe transversale basique de la structure démontre la Section Dorée. Si on attribue la valeur de 1 au demi-côté de la base, cela donne la valeur de phi à l’apothème, et la racine carrée de phi à la hauteur. La Section Sacrée est présente encore et encore à Giza de façon bien plus déroutante et assommante (des volumes entiers ont été rédigés au sujet des géométries appliquées à la construction des pyramides).

La suite de Fibonacci et la spirale d’or

Il existe une suite de nombres, connue sous le nom de suite de Fibonacci, qui a un rapport particulier avec phi, et les pyramides de Giza. Initialement postulée par le mathématicien médiéval Leonardo Fibonacci, cette suite été utilisée pour décrire les caractéristiques de la croissance des plantes.  La voici: 1,1,2,3,5,8,13,21,34,55,89,144,233, etc. Il faut ajouter les deux derniers nombres de la suite pour obtenir le suivant comme dans : 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, etc.

Le rapport entre cette suite et phi tient au fait qu’en divisant un terme de la suite par le suivant, le résultat approche rapidement le nombre transcendantal 1.6180339+...   (Je ne vous ferai pas faire de calculs. Observez simplement…)
1/1=1 2\1=2 3\2=1.5 5\3=1.66 13/8=1.625
21/13=1.615 34\21=1.619 55\34=1.617 89\55=1.6181
Plus on avance dans la suite, plus on se rapproche de phi. Bien-sûr, on ne l’atteint jamais avec exactitude, puisque c’est un nombre irrationnel, mais on ne cesse de s’en rapprocher à l’infini.

La suite peut être représentée graphiquement par la forme d’une spirale, qu’on appelle la Spirale de Fibonacci. La spirale est quasiment identique au graphique de la spirale logarithmique de la proportion phi, connue sous le nom de la Spirale d’Or. (La différence est que la spirale de Fibonacci est une interprétation en nombres entiers de la Spirale d’Or, arithmétiquement impossible, ayant ni début ni fin. La spirale de Fibonacci a un commencement défini).

La spirale de Fibonacci et les pyramides de Giza

Des prises de vues aériennes montrent que les pyramides de Giza sont positionnées de telle sorte qu’elles se trouvent sur une ligne qui représente avec exactitude une spirale de Fibonacci. La spirale passe exactement au centre de chaque pyramide.

Spirale d’Or or Prix: $977 USD

Spirale d’Or argent Prix: $115 USD

Spirale dorée argent petit Prix: $112 USD

Spirale dorée or petit Prix: $742 USD

Spirale dorée argent anneau Prix: $142 USD

Spirale dorée or anneau Prix: $1,778 USD

Pendentif Nautile or Prix: $648 USD

Pendentif Nautilus argent Prix: $120 USD