Espiral Dorado

"Quienquiera que cultive el medio dorado evita la pobreza del tugurio y la envidia de un palacio."
(Antiguo poeta romano)

Forma del Espiral Dorado

La estructura del Espiral Dorado representa dos formas famosas de la geometría Sagrada: el espiral medio dorado (phi) y el espiral Fibonacci. Se basa en la forma circular en un campo de cosecha conocido como “Formación Hackpen Hill " y apareció en el año 1999 en un campo de trigo en Inglaterra.

Phi (medio dorado) - "La llave a la física del cosmos” (Platón)

Phi es un valor constante que es aún más misterioso y profundo  en sus implicaciones que i pi. Como pi,  phi es un número sin solución aritmética. Los decimales simplemente continúan hasta la infinidad sin repetirse nunca. Lo único sobre este número es que puede ser incorporado en todas las estructuras orgánicas conocidas.  Desde la estructura ósea de los seres humanos hasta el diseño de las semillas del girasol y el espiral de una concha marina, la proporción phi está allí, subrayando todas las estructuras biológicas que parecieran ser un proyecto original geométrico para la vida misma.


Platón ha ido más allá y denominó a la relación phi la "llave a la física del cosmos”. Phi es calculado  a 1.6180339+..., y mientras no puede ser calculado aritméticamente, puede ser fácilmente obtenido con un compás y una regla.

El medio dorado en la arquitectura

La proporción phi se encuentra en la arquitectura de la Gran Pirámide en el triángulo formado por la altura, media base y apotema o diagonal. En otras palabras, la sección de la cruz básica de la estructura demuestra la Sección Dorada. Si la media base recibe el valor 1, se recibe el valor de phi para el apotema, y la raíz cuadrada de phi pr la altura. En Giza, la Sección Dorada se muestra nuevamente, y de manera mucho más desconcertante y tediosa (volúmenes completos han sido escritos sobre las geometrías involucradas en la construcción de las pirámides).

La secuencia Fibonacci y el espiral dorado

Existe una secuencia numérica conocida como la secuencia Fibonacci, la cual sostiene una relación especial a phi, y a las pirámides en Giza. Por vez primera fue postulada por el matemático medieval Leonardo Fibonacci, esta secuencia fue utilizada para describir el crecimiento de los patrones de las plantas. Es así: 1,1,2,3,5,8,13,21,34,55,89,144,233, etc. Se la hace al adherir los últimos dos números de la secuencia para recibir el siguiente, por ejemplo: 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13, etc.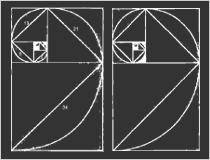

La relación de esta secuencia a phi es que si si se divide un término de la secuencia por el próximo, el resultado comienza rápidamente a acercarse al número trascendental 1.6180339+... (No les pediré hacer el cálculo, solo observad...)
1/1=1 2\1=2 3\2=1.5 5\3=1.66 13/8=1.625
21/13=1.615 34\21=1.619 55\34=1.617 89\55=1.6181
Cuanto más adelante se va en la secuencia, más cerca se llega a phi. Por supuesto, nunca se puede llegar exactamente a este, pues no posee solución aritmética, solo continua acercándose hasta la infinidad. 

La secuencia puede ser ilustrada en forma de espiral, llamado Espiral Fibonacci. Este espiral es casi idéntico al gráfico del espiral logarítmico de la proporción phi, conocido como el Medio del Espiral Dorado (la diferencia es que el espiral Fibonacci es la interpretación de un número entero del medio del espiral dorado que es aritméticamente imposible, que no posee comienzo o final. El espiral Fibonacci tiene un comienzo definido) 

El espiral Fibonacci y las pirámides de  Giza

Fotografías aéreas muestran que las pirámides de Giza están posicionadas de tal manera que caen sobre una línea que define exactamente un espiral Fibonacci. El espiral pasa exactamente por el centro de cada pirámide.

Espiral dorado- Oro Precio: $977 USD

Espiral dorado- Plata Precio: $115 USD

Espiral dorada de plata chico Precio: $112 USD

Espiral dorada de oro chico Precio: $742 USD

Anillo de plata de la espiral dorada Precio: $142 USD

Anillo de oro de la espiral dorada Precio: $1,778 USD

Nautilo oro Precio: $648 USD

Nautilo plata Precio: $120 USD